La belle verte – Adriano Sofo

L’articolo di questo mese, con un taglio di dossier, si pone l’obiettivo di analizzare, comprendere ed affrontare la delicata tematica relativa all’inquinamento del suolo, in modo particolare quello legato all’inquinamento derivante dall’abbandono dei rifiuti plastici, descrivendone le cause, gli effetti e le azioni da applicare per contrastare questo fenomeno sempre più frequente. Lo scopo è quello di contrastare gli effetti negativi sugli equilibri ambientali ed ecosistemici, applicando un metodo naturale e abbastanza efficace: il micorisanamento, ovvero l’impiego dei funghi “mangiatori di plastica”, che hanno dimostrato di essere in grado di ridurre al minimo la presenza di plastica all’interno del suolo e rendere così sani ed utilizzabili quei siti che prima versavano in condizioni di degrado. Verranno considerate anche altre tipologie di contaminanti che alterano le caratteristiche dei suoli e di come il micorisanamento possa essere utilizzato ai fini del ripristino delle condizioni ottimali dei suoli.

L’inquinamento del suolo costituisce una delle forme di inquinamento ambientale più grave e diffusa. Infatti, gli equilibri ambientali e la biodiversità sono strettamente connessi alla presenza di un suolo fertile e sano. Tra gli effetti più importanti, l’inquinamento del suolo può interessare la salubrità delle falde acquifere e le riserve d’acqua, influenzando così, inevitabilmente, anche la qualità degli alimenti. L’inquinamento del suolo consiste nella presenza di sostanze tossiche che ne alterano le caratteristiche. Esse possono essere di origine naturale o sintetica e, in molti casi, hanno effetti negativi sugli organismi viventi, con dirette conseguenze sulla catena alimentare, e la salute e il benessere umani. Questo tipo di inquinamento può essere anche meramente fisico. In questo caso è rappresentato dalle alterazioni del suolo che favoriscono smottamenti ed erosione e che, a loro volta, causano una diminuzione del suolo fertile.

Perdiamo circa 24 miliardi di tonnellate di suolo fertile all’anno. In Europa, la superficie agricola rappresenta il 25% di quella totale e circa l’80% contiene residui chimici di sintesi. Sempre in Europa, sono presenti circa 2,8 milioni di siti industriali di cui si sospetta la contaminazione. La scarsità di suolo fertile altera interi ecosistemi, innescando una grave tendenza alla desertificazione.

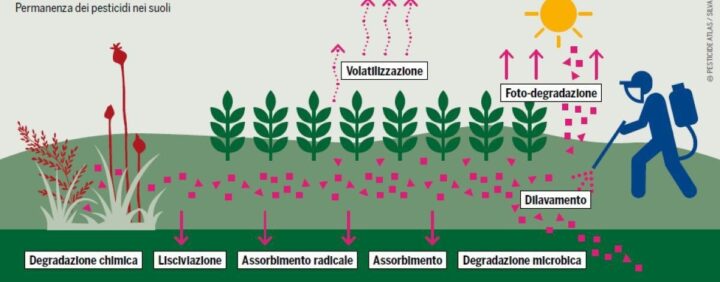
Tra le principali cause dell’inquinamento del suolo ci sono i rifiuti solidi, liquidi e gassosi, provenienti dalle attività antropiche. Oltre ai rifiuti domestici, ci sono quelli speciali derivanti dalle attività industriali, come per esempio idrocarburi e rifiuti contenenti diossine, metalli pesanti e solventi organici. Essi sono troppo spesso i protagonisti indiscussi di veri e propri disastri ambientali che alimentano il business degli ecoreati e il degrado ambientale, con gravi danni per la salute e l’ambiente. I prodotti fitosanitari utilizzati per combattere le principali avversità alle piante, in modo particolare nell’agricoltura intensiva, costituiscono uno dei principali responsabili dell’inquinamento del suolo. Essi causano anche inquinamento idrico e sono responsabili di danni alla salute umana a seguito alla loro ingestione. Causano, inoltre, malattie professionali agli agricoltori e a chiunque venga in contatto con queste sostanze.

L’estrazione dell’uranio, il riprocessamento e lo stoccaggio delle scorie radioattive generano anch’essi un inquinamento radioattivo. In aggiunta ci sono i disastri ambientali dovuti a malfunzionamenti e incidenti di impianti nucleari (Fukushima, Cernobyl, Three Mile Island, ecc.). A questi si aggiungono anche i residui inutilizzabili di scorie radioattive che vengono sepolti in fosse oceaniche profonde o, in alcuni casi, interrati in zone geologicamente sicure e stabili. 

 

Effetti della plastica sui suoli

Le plastiche sono contaminanti emergenti di relativamente nuova scoperta. Molto si è detto sull’inquinamento degli ambienti marini e fluviali, su cui sono già attivi e funzionanti molti progetti tesi al recupero delle plastiche. Tuttavia poco, anzi pochissimo, si conosce sull’inquinamento dei suoli. Perché? Se è relativamente semplice separare le particelle di plastica dall’acqua, non lo è nel suolo, e le tecnologie attualmente a disposizione non sono abbastanza accurate. Parallelamente, però, è sempre più evidente la presenza di plastiche nei suoli, la loro influenza sul funzionamento degli ecosistemi, il fatto che entrino nella catena alimentare sino ad attraversare addirittura la placenta degli animali.

Un terzo della plastica prodotta nel mondo finisce nel suolo, e si stima che la quantità di plastiche negli ecosistemi terrestri sia da 4 a 32 volte maggiore di quella presente negli oceani.

La crescita delle piante viene inibita dalle alte concentrazioni di plastica nel terreno. L’accumulo di residui plastici influenza anche l’idratazione del suolo, il trasporto dei nutrienti, l’attività dei microrganismi e la salinizzazione, contribuendo alla ritenzione di contaminanti, come i pesticidi. Le microplastiche diventano parte della struttura del suolo legandosi alle particelle organiche. Con l’erosione causata da acqua e vento, queste particelle possono addirittura essere trasportate in luoghi lontani, raggiungendo bacini idrici e oceani. Le microplastiche sono poi ingerite dalla micro e mesofauna del suolo, come vermi, parassiti, collemboli, enchitreidi, accumulandosi così nella catena alimentare, con un potenziale di biomagnificazione, fino ad arrivare agli uccelli che si nutrono di questi piccoli animali (FAO, Soil pollution: a hidden reality, 2018, www.fao.org/3/i9183en/ i9183en.pdf – N. R. Eugenio, 2018).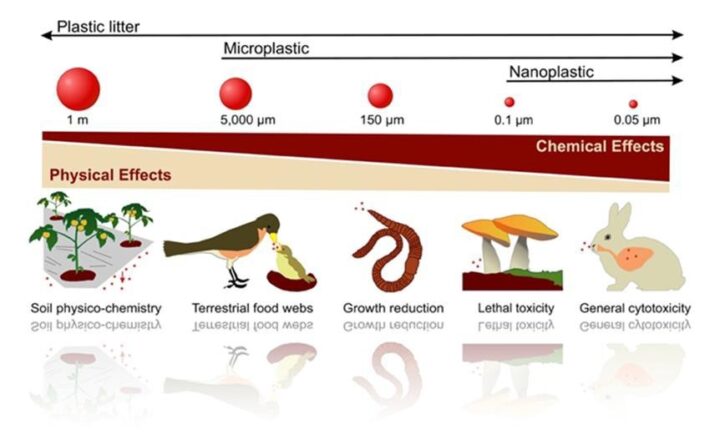

Effetti delle micro- e macroplastiche sulla catena alimentare

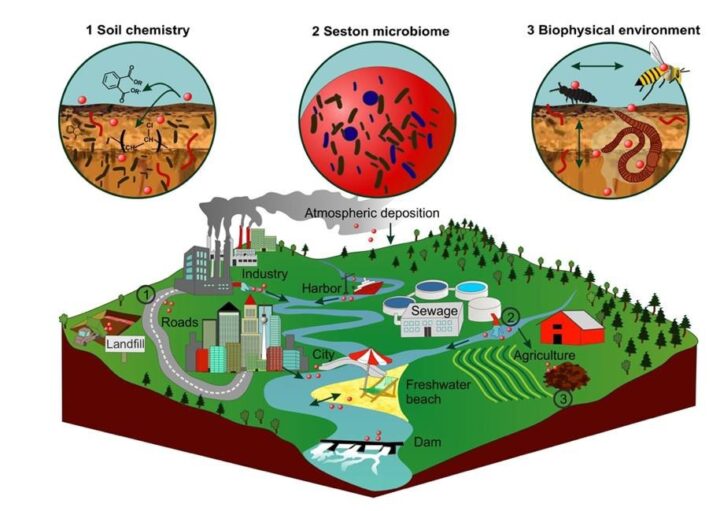Nella figura in alto sono visualizzate le zone dove sono presenti microplastiche in alta concentrazione: zone industriali, atmosfera, impianti di depurazione delle acque, terreni agricoli, spiagge, porti e dighe, città e strade, discariche (Global Change Biology, 2017). I tre cerchi in alto rappresentano uno zoom sugli effetti delle microplastiche sulla composizione chimica nel suolo (Fuller & Gautam, 2016), sul microbioma del suolo (Mccormick et al., 2016) e sull’ambiente biofisico (Huerta Lwanga et al., 2017; Liebezeit & Liebezeit, 2015; Maass et al., 2017; Rillig, Ziersch, et al., 2017; Zhu et al., 2018).

Foraggio rivestito con pellicola plastica per riparo dalle intemperie

La plastica è onnipresente in agricoltura. Infatti, le macroplastiche sono utilizzate come involucri protettivi attorno a pacciame e foraggi, coprono le serre e proteggono le colture dagli elementi, vengono utilizzate nelle tubazioni per l’irrigazione, sacchi e contenitori. Le microplastiche, invece, vengono aggiunte intenzionalmente ed utilizzate come rivestimenti su fertilizzanti, pesticidi e semi.

“C’è solo una quantità limitata di terreno agricolo disponibile” – ha affermato Elaine Baker, Professoressa di Scienze Marine presso l’Università di Sydney e Direttrice ufficio GRID-Arendal (partner dell’UNEP) presso la stessa Università. “Stiamo iniziando a capire che l’accumulo di plastica può avere impatti ad ampio raggio sulla salute del suolo, sulla biodiversità e sulla produttività, tutti elementi vitali per la sicurezza alimentare”.

Nel tempo, le macroplastiche si decompongono lentamente in microplastiche di frammenti lunghi meno di 5 mm e penetrano nel terreno. Queste microplastiche possono modificare la struttura fisica del suolo e limitarne la capacità di trattenere l’acqua. Ciò può influenzare le piante, riducendo la crescita delle radici e l’assorbimento dei nutrienti. Gli additivi chimici nella plastica che filtrano nel suolo possono anche avere un impatto sul valore degli alimenti e portare a implicazioni per la salute, entrando nella catena alimentare.

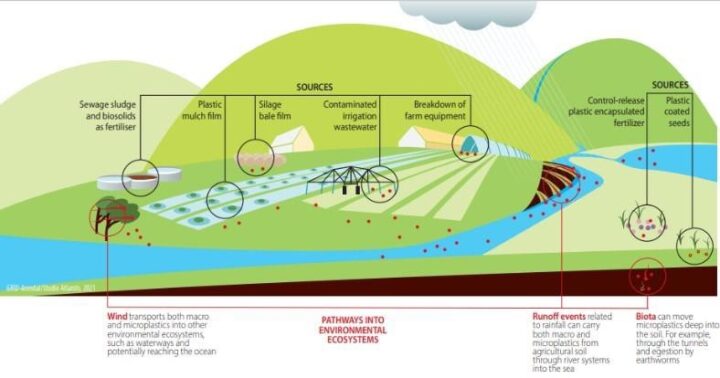
La principale fonte di inquinamento da microplastica nel suolo sono i fertilizzanti prodotti con materia organica, come il letame, conosciuti come biosolidi, che dovrebbero essere più salubri per l’ambiente rispetto ai fertilizzanti di sintesi. Purtroppo nel letame si mescolano le microsfere, le minuscole particelle sintetiche comunemente utilizzate nel sapone, shampoo, trucco e altri prodotti per la cura personale, il che è motivo di preoccupazione. Esempi di fonti e trasporto di plastica e co-contaminati dalla produzione agricola all’ambiente (Fonte: “Plastics in agriculture: sources and impacts”, 2021).

Secondo uno studio, pubblicato il 1° luglio 2022 su Environmental Pollution e condotto da ricercatori dell’Università di Cardiff, i terreni agricoli d’Europa sono potenzialmente il più grande serbatoio globale di microplastiche a causa delle alte concentrazioni presenti nei fertilizzanti derivati dai fanghi di depurazione. Ogni anno, sui suoli dei terreni agricoli europei, sarebbero sparse tra le 31.000 e le 42.000 tonnellate di microplastiche.

Alcuni Paesi hanno vietato le microsfere di plastica, ma molte altre continuano ad entrare nel sistema idrico (nell’UE il divieto è scattato dal 1° gennaio 2021, ma in Italia è stato anticipato di un anno, valido solo per gli esfolianti e i detergenti a risciacquo), tra cui quelle dei filtri delle sigarette, dei sistemi di abrasione degli pneumatici e quelle derivanti dalle fibre sintetiche dei vestiti. Gli esperti affermano che le dimensioni e le composizioni variabili delle microplastiche le rendono difficili da rimuovere una volta che sono nelle acque reflue.

Attualmente, si stanno compiendo progressi per migliorare la biodegradabilità dei polimeri utilizzati nei prodotti agricoli. Alcuni teli per pacciamatura, utilizzati per modificare la temperatura del suolo, limitare la crescita delle erbe infestanti e prevenire la perdita di umidità, vengono ora commercializzati come completamente biodegradabili e compostabili, ma ciò non è sempre vero. Inoltre, i ricercatori sottolineano che la produzione di polimeri a base biologica non dovrebbe generare concorrenza per il suolo con quella utilizzata per produrre cibo. Possono essere utilizzate anche le cosiddette colture di copertura, che proteggono il suolo e non sono destinate alla raccolta. Queste soluzioni basate sulla natura (nature-based solutions, NBS) possono sopprimere le malerbe, contrastare le malattie del suolo e migliorarne la fertilità, ma si teme che possano ridurre i raccolti e aumentare i costi.

“Nessuna di queste soluzioni è una bacchetta magica – ha aggiunto Baker – La plastica è economica e facile da lavorare, il che rende difficile provare a introdurre alternative “.

Secondo la ricercatrice, i governi devono “disincentivare” l’uso della plastica in agricoltura, seguendo il percorso dell’UE che ha limitato l’uso di alcuni tipi di polimeri nei fertilizzanti. Baker ha anche affermato che sono necessarie ulteriori ricerche per sviluppare prodotti, come alcuni tessuti alternativi, che non perdano microplastiche, mentre i consumatori dovrebbero essere incoraggiati a riconsiderare il loro consumo di plastica e i produttori a ridurre la quantità di plastica che usano.

“Sebbene ci siano molte ricerche limitate all’impatto della plastica nel suolo, ci sono già prove di effetti negativi sulla salute e sulla produttività del suolo – ha concluso la ricercatrice – Ora è il momento di adottare il principio di precauzione e sviluppare soluzioni mirate per fermare il flusso di plastica dalla fonte e nell’ambiente”.

 

Il micorisanamento

Le complesse dinamiche che caratterizzano l’habitat dei suoli, costituiscono un ostacolo non indifferente alla ricerca scientifica, determinando una discrepanza tra i dati disponibili utili a stabilire l’entità dei danni e il tipo di intervento più idoneo al risanamento dei siti contaminati dalle diverse forme di inquinamento de suolo.

Il biorisanamento è una NBS che si basa sul metabolismo microbico di microrganismi, ambientali o artificiali, capaci di biodegradare e detossificare le sostanze inquinanti. Le diverse tecniche di micorisanamento si possono applicare in situ o in ex situ.

Le materie plastiche prodotte dalle diverse attività antropiche sono molteplici, con altrettante caratteristiche fisico-meccaniche, e la loro presenza in ambienti terresti deriva principalmente da fanghi attivi smaltiti in campo, teli di pacciamatura, irrigazione con acque reflue, inondazioni, ricadute atmosferiche, abrasione degli pneumatici, scarico illegale di rifiuti, ecc. Arrivate nell’ambiente, le plastiche hanno un impatto su tutti gli organismi viventi, causandone danni fisici e fisiologici, sino a provocarne la morte.

Secondo un rapporto della Commissione Europea ogni anno inaliamo o ingeriamo dalle 39.000 alle 52.000 particelle plastiche l’anno, l’equivalente di una carta di credito. Su queste premesse, la pratica del micorisanamento costituisce una valida soluzione alla riduzione di tali inquinanti nel suolo.

Le mascherine chirurgiche impiegano fino a 450 anni per decomporsi totalmente

Per secoli, i funghi che sono stati impiegati come prodotto alimentare proveniente dal bosco o da funghicoltura, oltre ad essere caratterizzati da esclusive proprietà aromatiche, organolettiche e proteiche, si sono rivelati essere più che semplici prodotti alimentari. Infatti, è stato scoperto che i funghi hanno una propensione unica a scomporre gli inquinanti, inclusi petrolio e pesticidi, e a estrarre o legare metalli pesanti, fino a contrastare persino le radiazioni (Ali & Di, 2017). I funghi sono inoltre in grado di filtrare l’acqua, supportando innumerevoli cicli vitali rigenerativi per gli ecosistemi.

Il micorisanamento è un metodo che utilizza il micelio dei funghi (la parte vegetativa di un fungo) in siti di terreno contaminati come trattamento riparatore. Gli enzimi prodotti da un fungo sono efficaci nell’abbattere molti diversi inquinanti. In sostanza, questo metodo sfrutta le naturali capacità di decomposizione dei funghi per ripristinare e rigenerare il terreno.

L’accumulo di metalli pesanti e sostanze chimiche tossiche nel nostro ambiente è un problema grave e sempre persistente. Queste tossine finiscono nella nostra catena alimentare (come metalli pesanti, PCB e diossine) e vanno incontro a bioaccumulo, ovvero l’accumulo graduale di una determinata sostanza chimica nel tessuto vivente di un organismo dal suo ambiente che può derivare dall’assorbimento diretto dall’ambiente o dall’ingestione di particelle di cibo. I miceli fungini possono rimuovere queste tossine nel terreno prima che possano entrare nelle nostre riserve di cibo e, infine, nel nostro corpo.

Il micelio è la parte vegetativa dei funghi: si tratta di filamenti bianchi sotterranei, chiamati ife, con una struttura siile a quelle delle radici e delle ragnatele, i quali sono colonizzano i suoli e altri ambienti ricchi di umidità, come i tronchi di alberi in decomposizione. Le ife sono deputate all’assorbimento di acqua e nutrienti.

Il micelio può essere persino resistente al fuoco e si è rivelato uno strumento straordinario per gli sforzi di risanamento ambientale. Alcune specie di funghi vengono addirittura “addestrate” nei laboratori per digerire rifiuti plastici, come mascherine polipropilene e guanti di plastica (Alexander, 2019). La maggior parte della degradazione avviene prima che si formi il corpo fruttifero; le tossine e i rifiuti vengono completamente assorbiti dal fungo in genere entro poche settimane (Alexander, 2019), un dato molto incoraggiante, visto che il tempo di degradazione delle plastiche nel suolo si può protrarre per decenni o secoli.

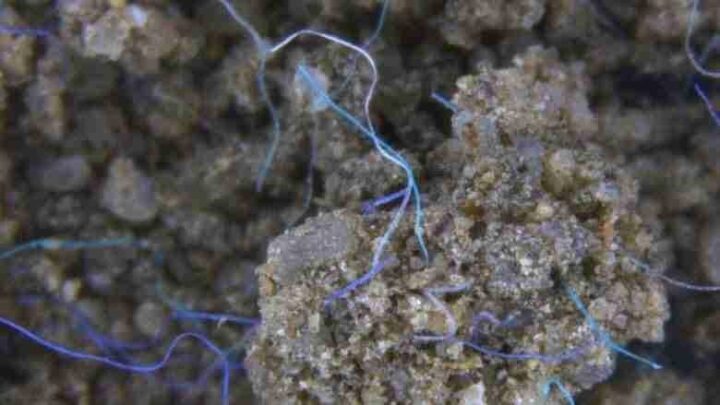
Micelio fungino

Il processo con cui i funghi decompongono la plastica coinvolge una famiglia di enzimi chiamati laccasi, i quali scompongono i polimeri in molecole più piccole, che possono poi essere assorbite dal fungo. Questo processo richiede da due settimane a diversi mesi, a seconda del tipo di plastica utilizzata.

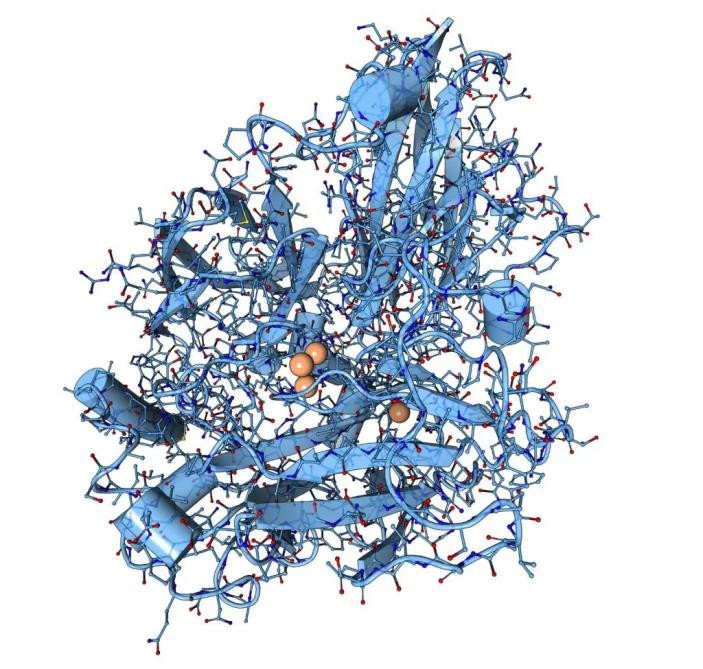
Struttura tridimensionale di una laccasi

I funghi utilizzano una combinazione di enzimi per scomporre le catene di polimeri che costituiscono la plastica. Gli enzimi lavorano insieme ad altri microrganismi, come i batteri, per accelerare il processo. Oltre a scomporre la plastica, questi funghi rilasciano anche sostanze nutritive nel terreno, favorendo la crescita delle piante. Le laccasi sono in grado di scomporre le molecole più grandi in molecole molto più piccole, le quali possono essere assorbite dal fungo stesso o da altri microrganismi che vivono nel suolo. Infatti, i funghi si sono evoluti nel corso di milioni di anni per scomporre molecole complesse in componenti più semplici e più facili da metabolizzare. Questo processo è noto come biodegradazione: gli enzimi prodotti dai funghi rompono i legami tra gli atomi dei polimeri per rimpicciolirli e assorbirli nelle loro cellule. Come avviene per gli enzimi digestivi dell’uomo, i funghi digeriscono i polimeri.

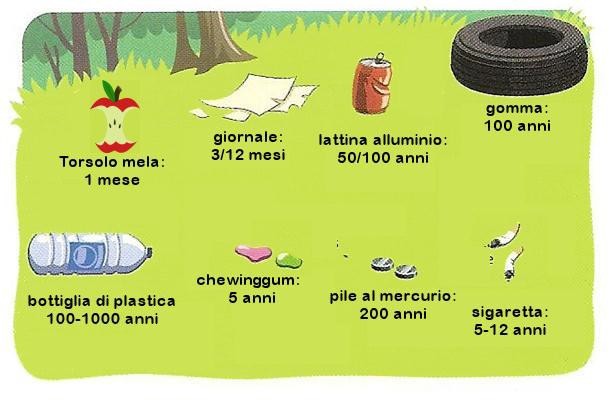Tempi di degradazione di diverse tipologie di rifiuti

 

Il ruolo dei batteri nel micorisanamento

Oltre ai funghi, anche i batteri svolgono un ruolo importante nel micorisanamento. Le popolazioni batteriche si affiancano a quelle fungine e contribuiscono a facilitarne i processi di decomposizione, producendo enzimi aggiuntivi che abbattono ulteriormente i polimeri. Questa categoria di batteri in grado di scomporre gli agenti contaminanti presenti nel suolo, comprende anche i batteri idrocarburoclastici (da qui la sigla BIC), ovvero organismi che si “nutrono” di petrolio utilizzandolo per i loro processi metabolici. I batteri secernono anche acidi organici che aiutano a sciogliere alcuni tipi di plastica e agiscono come catalizzatori per la produzione di enzimi fungini. Questa relazione simbiotica tra batteri e funghi rende il micorisanamento uno strumento ancora più efficace.

 

Funghi che degradano la plastica

Attualmente sono state identificate diverse specie di funghi mangiatori di plastica. Ognuna di esse presenta capacità più o meno accentuate nello scomporre diversi tipi di plastica, ma tutte e tre condividono alcuni tratti comuni.

Pestalotiopsis microspora

Questa specie è stata scoperta per la prima volta nei terreni della foresta amazzonica ecuadoriana, dove è stata osservata mentre decomponeva campioni di poliuretano espanso nel giro di poche settimane. È in grado di digerire sia le pellicole di polietilene a bassa densità (LDPE) comunemente utilizzate per gli imballaggi alimentari, sia le pellicole di polietilene ad alta densità (HDPE) tipicamente utilizzate per la produzione di bottiglie.

Pleurotus ostreatus e Schizophyllum commune 

L’inquinamento da plastica è una crisi globale e la scoperta dei funghi “mangiaplastica” è stata accolta come una soluzione rivoluzionaria. Due specie di funghi che si sono dimostrate promettenti in questo campo sono il Pleurotus ostreatus (il comune cardoncello) e lo Schizophyllum commune. Sul cardoncello ci ho lavorato anche io qualche anno fa e abbiamo pubblicato questo lavoro in cui è stato dimostrato che questo fungo è in grado di degradare persino sostanze medicinali.

Pleurotus ostreatus

Entrambi sono in grado di digerire il poliuretano, uno dei principali componenti di alcune plastiche. Sebbene siano necessarie da due settimane a diversi mesi per scomporre la plastica, a seconda del tipo utilizzato, questi funghi potrebbero essere uno strumento efficace per la bonifica dei rifiuti plastici.

Schizophyllum commune

Aspergillus tubingensis 

Aspergillus tubingensis è un’altra specie che ha la capacità di degradare poliuretano. È stata scoperta nel 2018 dai ricercatori dell’Università di Kyoto e da allora è diventata uno strumento importante per la bonifica dei rifiuti plastici. Questa particolare specie di funghi impiega circa due settimane per scomporre e consumare la plastica, a seconda del tipo di plastica utilizzata. Questo lo rende un efficiente digestore per sbarazzarsi efficacemente dei rifiuti di plastica.

 

Ma i funghi “mangiaplastica” sono commestibili?

La risposta breve è no: Aspergillus tubingensis e altri funghi mangiatori di plastica non sono commestibili e non dovrebbero essere consumati. Tuttavia, alcuni di essi, come il comune cardoncello, possono essere consumati. Inoltre, la ricercatrice australiana Katharina Unger ha creato un prototipo chiamato Fungi Mutarium che può essere utilizzato per coltivare questi funghi commestibili in grado di degradare plastica. Fungi Mutarium, un progetto di Livin Studio in collaborazione con l’Università di Utrecht, è un prototipo per coltivare una biomassa fungina commestibile, principalmente miceli, come un nuovo prodotto alimentare.

 

I potenziali benefici del micorisanamento

Il micorisanamento è un processo che prevede l’utilizzo di funghi per scopi di bonifica, come la degradazione di sostanze inquinanti quali gli idrocarburi derivanti dal petrolio (vedete, se vi va, questo lavoro che ho pubblicato qualche anno fa) o i policlorobifenili (PCB). Lo stesso processo può essere applicato alla plastica utilizzando alcune specie di funghi che si sono evolute nel tempo con la capacità di scomporre le catene di polimeri in composti più piccoli. Utilizzando le tecniche di micorisanamento, i ricercatori possono coltivare ceppi specifici di funghi che si nutrono di materiali sintetici come la plastica. Creando un ambiente in cui questi funghi possano prosperare, gli scienziati sperano che i loro sforzi portino a metodi più efficaci per scomporre i materiali artificiali in modo più rapido che mai. Grazie al micorisanamento, potremmo aver trovato un potente strumento per ridurre la nostra dipendenza dalla plastica e salvare il nostro pianeta!

Tra i benefici si possono annoverare:

• Riduzione della necessità di spazio in discarica, grazie alla diminuzione della quantità di materiali non biodegradabili che vengono
• Fonti d’acqua più pulite, grazie alla riduzione della lisciviazione dalle discariche nei corpi idrici
• Uso più efficiente delle risorse, grazie alla trasformazione di ciò che altrimenti sarebbe un rifiuto in materiale

Utilizzando il micorisanemento, potremmo potenzialmente creare un’economia sostenibile e circolare basata sulla coltivazione dei funghi.

Un tipo di economia che ci aiuterebbe a ridurre la nostra dipendenza da materiali non biodegradabili, fornendoci al contempo fonti di cibo. Questo potrebbe rivoluzionare il nostro approccio alla soluzione di problemi ambientali globali, come l’inquinamento da plastica, migliorando al contempo i risultati in termini di salute della collettività.

 

Micorisanamento applicato ad altre tipologie di contaminanti

“Già in passato, i funghi hanno dimostrato grande capacità di sopravvivere e anzi di prosperare di fronte a mutamenti ambientali di grande portata: i funghi che decompongono il legno ebbero un ruolo importante nella transizione da un’epoca chiamata Carbonifero, in cui a causa dell’assenza di decompositori di lignina, il grande accumulo dei resti di alberi nel sottosuolo era stato causa di un importante cambiamento climatico. Proprio grazie alla loro capacità “decostruttiva” questi organismi hanno dimostrato capacità di sopravvivere alle devastazioni ambientali. Non soltanto la lignina, ma numerosi altri inquinanti possono essere digeriti e usati come fonte di sostentamento dai funghi: dai mozziconi di sigaretta ai pesticidi, a vari tipi di rifiuti agricoli, i funghi sanno trasformare vari inquinanti pericolosi per la vita umana e ripristinare ecosistemi gravemente danneggiati. I limiti relativi a queste pratiche di micorisanamento dipendono in larga parte dalla complessità di questi organismi: i funghi proliferano in modo irriducibilmente imprevedibile, così come il loro comportamento rispetto agli inquinanti rimane complesso. Il micorisanamento si configura come una forma di “digestione esterna”, o un’esternalizzazione di processi digestivi: un’associazione in cui organismi diversi intonano insieme una canzone metabolica che da soli non saprebbero cantare. In questa relazione, i funghi si configurano sia come tecnologie, che come partner degli esseri umani.”

Agganciandosi a questo concetto proposto da Merlin Sheldrake, biologo e scrittore naturalista, ci si rende conto di quanto sia vasto e complesso il mondo dei funghi, di come sia fondamentale la loro presenza negli ambienti per il mantenimento degli equilibri ecosistemici e di quanto siano variegate le loro funzioni in natura.

Oltre ad essere una pratica efficace e risolutiva, il micorisanamento trova impiego nel trattamento dei siti che oltre ad essere soggetti ad inquinamento plastico sono alterati dalla presenza di altri contaminanti. Ripristinare il suolo contaminato decomponendo le sostanze tossiche e risolvendo, alla base, il problema dello smaltimento è la missione di un interessante progetto dell’University of Wisconsin-Stevens Point che vede per protagonisti proprio i funghi. Oggetto della sperimentazione è stato un blocco di terra carico di petrolio. A novembre i ricercatori hanno iniziato a coltivarci funghi di buona qualità, con risultati sorprendenti. La terra non trattata si presentava fortemente odorosa di petrolio, mentre dove i funghi sono stati coltivati e cresciuti, invece, il suolo ha iniziato ad avere un buon profumo, un indizio che potrebbe essere il preludio di risultati interessanti.

Sito inquinato da sversamento di petrolio

L’olfatto, ovviamente, non fornisce una prova definitiva. Ma gli studiosi ritengono che le analisi di laboratorio possano confermare l’ipotesi più ottimistica. La speranza, insomma, è che i funghi abbiano saputo portare a termine il loro compito “ripulendo” di fatto il terreno dalle sostanze nocive che avrebbero potuto renderlo inutilizzabile.

Anche nei casi più critici di inquinamento del suolo non mancano i vantaggi. Per esempio, nel suolo contaminato da metalli pesanti, i funghi assorbono le sostanze nocive diventando a loro volta tossici. Ad essere ripristinato però è il terreno che, di conseguenza, non deve più essere bonificato. A quel punto, quindi, lo smaltimento riguarda solo i funghi. Con conseguente risparmio di spazio in discarica. Grazie a questo processo è quindi possibile ridurre i costi di smaltimento. Nel corso degli anni, gli esperimenti non sono mancati. Il micorisanamento è stato utilizzato anche per decontaminare i terreni dai pesticidi. Si trovano, infatti, studi di come i funghi riescano a scomporre pesticidi e molti farmaci. Paul Stamets, nel suo libro “Mycelium Running”, descrive molto bene come i funghi Trametes spp. e Psilocybe azurescens riescano a scomporre addirittura una potente neurotossina, il dimetilfosfonato. Grazie a queste capacità, il micelio della coltivazione di funghi, si presenta anche come la soluzione per filtrare l’acqua da Escherichia coli, colera, Listeria e altri agenti patogeni; fosfati, fertilizzanti, interferenti endocrini, metalli pesanti e rifiuti tossici a base di petrolio. Nel 2017, inoltre, alcuni ricercatori cinesi hanno isolato un altro fungo in grado di digerire il poliuretano. Pare, infatti, che ci sia un fungo, il Pestalotiopsis microspora, che ha una caratteristica molto particolare: si nutre quasi esclusivamente di poliuretano. Questo materiale è un polimero plastico particolarmente resistente, utilizzato in molteplici contesti, che si decompone in modo spontaneo nel giro di centinaia di anni. Sedili, tubi, imbottiture, imballaggi: il poliuretano è praticamente ovunque, ma con questo fungo la sua permanenza nell’ambiente potrebbe essere ridotta, e di molto. Ciò che differenzia il Pestalotiopsis dagli altri funghi in grado di “aggredire” la plastica è che può farlo anche in ambienti anaerobici, dunque senza ossigeno. Questo vuol dire che, potenzialmente, potrebbe crescere e proliferare anche in luoghi come fondi di discariche, dando un aiuto fondamentale a degradare più velocemente le inquinanti materie plastiche. I benefici e i vantaggi di questo utile organismo naturale scoperta sono stati descritti dal team di scienziati di Yale in un articolo pubblicato sulla rivista Applied and Environmental Microbiology. I ricercatori hanno fatto sapere che sono riusciti a isolare l’enzima che il fungo usa per sciogliere il legame del poliuretano, la serina idrolasi.

L’efficacia di queste tecniche, tuttavia, appare ancora variabile e sembra essere condizionata da tanti fattori. Proprio per questo, saranno necessarie ulteriori ricerche negli anni a venire per esplorare le opportunità di una strategia che resta in ogni caso promettente. È stato osservato, infatti, che alcuni interventi con Pleurotus spp. hanno avuto pieno successo nel degradare gas sarin e alcuni gas nervini. I fattori fisici che influenzano tali processi sono la temperatura, la presenza di ossigeno ed il pH (i funghi preferiscono lavorare in condizioni di pH acido).

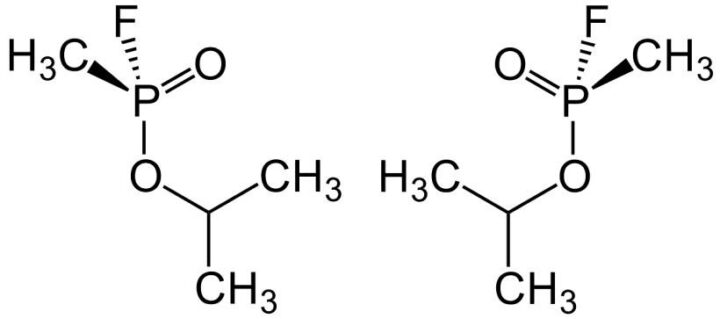
Gas nervino

Altri risultati soddisfacenti, utilizzando funghi dello stesso genere, sono stati ottenuti in un terreno contaminato da gasolio sottoposto a pratica di micorisanamento. Dopo quattro settimane più del 90% degli idrocarburi policiclici aromatici (IPA) è stato degradato a componenti non tossici, anche grazie alla sinergia che si era creata con la flora microbica naturale presente nel terreno.

 

Conclusioni

Il potenziale dei funghi come risorsa sostenibile nella lotta contro l’inquinamento da plastica ha preso sempre più piede negli ultimi anni. Con la scoperta di nuove specie di funghi in grado di scomporre diverse sostanze inquinanti o di digerire il poliuretano, scienziati e imprenditori stanno esplorando modi per sviluppare un’economia basata su questi funghi “mangiaplastica”. Da questo ne scaturisce che la coltivazione dei funghi non è solo un’opzione valida per ridurre i rifiuti di plastica ma potrebbe anche creare posti di lavoro e offrire opportunità economiche alle comunità colpite dall’inquinamento da plastica.

L’excursus dei funghi mangiaplastica è stato finora un’incredibile storia di successo. Dai loro umili inizi come semplici funghi che crescevano in natura a fenomeno globale. Non solo questi funghi stanno aiutando a ridurre la quantità di inquinamento da plastica nell’ambiente ma potrebbero costituire in futuro una fonte di nutrimento sostenibile e rinnovabile per le diverse popolazioni del mondo o per le generazioni future. Con ulteriori ricerche e sviluppi, questa tecnologia rivoluzionaria potrebbe un giorno fornirci un modo davvero sostenibile per ridurre la nostra dipendenza dalla plastica e i suoi effetti negativi sull’ambiente.

Nel lontano 2016, avevamo parlato qui di indici basati sul té. Ebbene, il progetto è andato avanti grazie al lavoro di ricercatori e cittadini comuni sparsi in tutto il mondo. Nei giorni scorsi, abbiamo finalmente ricevuto l’accettazione del nostro lavoro su Ecology Letters (Reading tea leaves worldwide: decoupled drivers of initial litter mass-loss rate and stabilization. doi: 10.1111/ele.14415), abbiamo reso pubblici i nostri risutati grezzi nel research repository pubblico Zenodo e, dulcis in fundo, abbiamo aggiunto e stiamo aggiungendo una miniserie di interviste (Tea Tales) sulle nostre esperienze con le tea bags e sulle loro ricadute pratiche (qui trovate anche la mia).

Grazie di cuore a tutti i partecipanti di questa bellissima e costruttiva esperienza di citizen science.

 

In un contesto urbano sempre più dominato da strutture di cemento e asfalto, la crescente consapevolezza dell’importanza del verde nelle città sta promuovendo una rivoluzione silenziosa. Ci sono oramai esempi concreti in tutto il mondo sul ruolo cruciale che il verde urbano svolge nel plasmare il nostro ambiente e il benessere umano. Il verde in città porta con sé una serie di benefici diversificati, noti come servizi ecosistemici, che influenzano positivamente sia l’ambiente che il benessere delle persone. Le piante assorbono gas nocivi, come l’anidride carbonica e altri inquinanti atmosferici, contribuendo a migliorare la qualità dell’aria nelle aree urbane.

Inoltre, gli alberi e le aree verdi possono fornire ombra, riducendo gli effetti delle isole di calore urbane e contribuendo a mantenere temperature più basse nelle città, specialmente durante i periodi caldi, quando gli alberi evapotraspirano di più. Inoltre, la presenza di verde in città favorisce la biodiversità, fornendo habitat per una varietà di specie vegetali e animali, promuovendo così l’equilibrio degli ecosistemi urbani. Il verde urbano assorbe anche l’acqua piovana, riducendo il rischio di allagamenti e contribuendo alla sostenibilità delle città. Alberi piantati strategicamente possono offrire ombra agli edifici, riducendo la necessità di raffreddamento artificiale e portando a risparmi energetici. Dal punto di vista del benessere umano, la presenza di verde in città è associata a una migliore salute mentale e fisica. Passeggiare in parchi o giardini può ridurre lo stress, migliorare il tono dell’umore e promuovere un senso di benessere generale. L’agricoltura urbana e gli orti comunitari contribuiscono alla sostenibilità alimentare, offrendo un accesso locale a prodotti freschi e promuovendo uno stile di vita più sano. Inoltre, spazi verdi ben progettati rendono le città più attraenti, invitando le persone a godere degli spazi pubblici e contribuendo a una maggiore coesione sociale. Gli alberi e le piante agiscono anche come barriere naturali contro il rumore urbano, fornendo un ambiente più tranquillo e rilassante. In sintesi, integrare il verde nelle città non solo migliora l’aspetto estetico, ma fornisce una serie di vantaggi tangibili che contribuiscono alla sostenibilità ambientale e al benessere delle comunità urbane.

Tra le città virtuose in tal senso, Singapore ha recentemente inaugurato il Singapore Green Plan 2030. Si tratta di un movimento nazionale per portare avanti l’agenda nazionale di sviluppo sostenibile di Singapore attraverso cinque pilastri principali: Città Natura, Vita Sostenibile, Rilancio Energetico, Economia Verde e Futuro Sostenibile. Per raggiungere questi obiettivi, il governo di Singapore introdurrà una serie di nuove iniziative e obiettivi nei settori della finanza verde, della sostenibilità, dell’energia solare, dei veicoli elettrici e dell’innovazione. Gli incentivi possono essere utilizzati per incoraggiare lo sviluppo e la diffusione di tecnologie nel campo dell’energia solare, dei veicoli elettrici e di altri settori della finanza verde. Gli incentivi forniti dal governo di Singapore possono dare alle aziende singaporiane la vitalità di cui hanno bisogno per avviare joint venture con aziende globali esistenti o per diventare leader di mercato in futuro. Singapore, con il suo progetto di “Città Giardino”, è un esempio paradigmatico. I giardini verticali e le iniziative di piantumazione massiccia hanno trasformato la città, riducendo la temperatura urbana e contribuendo alla qualità della vita.

Città come Portland, San Francisco e Vancouver stanno adottando politiche urbane incentrate sulla sostenibilità. Programmi di riforestazione urbana, parchi accessibili e la creazione di corridoi verdi contribuiscono significativamente al benessere urbano. In Giappone, la città di Kitakyushu ha investito in progetti di riforestazione su vasta scala, dimostrando come il verde in città possa fungere da strumento di adattamento ai cambiamenti climatici. Altri esempi salienti includono Oslo, con il suo impegno per una “città verde entro il 2030”, e Copenaghen, con la sua rete estensiva di piste ciclabili e spazi aperti. La strada considerata come la “mais bonita do mundo” è in Brasile a Porto Alegre e, se è così bella, il perché lo trovate in questo sito.

Durante i miei viaggi, mi sono sempre sorpreso di vedere come metropoli e capitali (mi vengono in mente, tra le tante, Tel Aviv, San Francisco, Tokyo, Amsterdam, Berlino, Bruxelles, ecc.), stiano investendo sempre di più in questi progetti verdi, mentre in Italia si è enormemente indietro e ogni tentativo di introdurre piante e spazi aperti è quasi sempre fortemente osteggiato, adducendo le più svariate giustificazioni (alberi che cadono in testa e sulle macchine, foglie che intasano i tombini, invasioni animali cittadine, radici che distruggono l’asfalto, costi di manutenzione alti, necessità di case, ecc.). Spesso queste argomentazioni, nel migliore dei casi, sono basate sull’ignoranza dei numerosi benefici degli alberi e delle zone verdi in città; inoltre, di nuove case non ce ne sarebbe proprio bisogno, dato l’enorme calo demografico italiano, né tantomeno sarebbero necessarie molte auto se ci fosse un trasporto pubblico capillare e integrato. Molto spesso, tali scuse sono invece mosse da forti interessi delle amministrazioni locali, che evidentemente ricavano molto di più dall’edificazione di nuove aree e dagli appalti di strade, cemento e asfalto. Il tutto è condito da una scarsa pressione dal basso da parte dei cittadini, che pagano ingenti tasse comunali ma non pretendono aree verdi nelle loro città. I cittadini poi pagano di tasca loro tutti i servizi (energia elettrica per condizionatori, manutenzione di strade a causa dell’enorme tarffico cittadino, parchi gioco e ludoteche private, costi per palestre e ansiolitici, servizi per animali da compagnia, ecc.), che invece gli spazie verdi fornirebbero gratuitamente. Nella città in cui vivo, Trani, ci si affida a fior di consulenze per mappare i pochi alberi e per identificare quelli in presunte cattive condizioni (e si pagano i consulenti), si tagliano questi alberi (e si pagano i tagliatori), si potano – male – quelli sani (e si pagano i potatori), ma stranamente non se ne piantano mai di nuovi, mentre le aree disboscate vengono poi prontamente edificate o cementificate (dei pericoli del soil sealing ne avevo parlato qui).

Persino negli industrializzati USA, ci sono esempi virtuosi e paradigmatici. A Davis, in California, mi è capitato di andare a trovare un amico, il quale mi ha raccontato la storia del suo quartiere, Village Homes, attivo dagli anni ’80, con 225 case e 20 appartamenti. Il progetto presenta un’organizzazione urbana innovativa. L’orientamento delle strade e dei lotti, seguendo l’asse est-ovest e nord-sud rispettivamente, massimizza l’utilizzo dell’energia solare. Il design delle strade, con numerosi vicoli ciechi, rende meno attraente l’uso dell’auto, promuovendo percorsi pedonali verso il centro della città. Le vie seguono avvallamenti dove l’acqua piovana è indirizzata per irrigare piante e alberi, inclusi frutteti e vigneti. Le strade sono strette e prive di marciapiedi, con cul-de-sac curvati, riducendo l’esposizione al sole. Le linee curve delle strade limitano la velocità delle auto. Percorsi pedonali e ciclabili alternati alle strade attraversano aree comuni con giardini, strutture ludiche e opere d’arte. Le abitazioni si affacciano su queste aree, accentuando l’importanza di spostamenti a piedi e in bicicletta. Il sistema innovativo di drenaggio naturale, con letti di ruscelli e lagune, trattiene l’acqua piovana nel terreno, contribuendo alla conservazione dell’umidità e offrendo un elemento visivamente interessante. Gli spazi verdi sono anche funzionali, nel senso che ci sono alberi da frutto e noci, con oltre 30 varietà piantate per garantire frutti maturi praticamente ogni mese. Aree verdi produttive e ornamentali, gestite dai giardinieri, sono collocate lungo i percorsi pedonali principali. Terre agricole comprendono giardini, orti e vigneti, con il 24% del cibo coltivato nelle strade e negli orti. Il progetto include diverse soluzioni abitative e ampie aree verdi, con il 40% del terreno di proprietà comune. Purtroppo, nonostante il successo dimostrato indicano il Village Homes come modello ideale di design urbano, pochi hanno replicato il progetto in oltre 30 anni, per ragioni rimaste oscure. Qui in basso, il quartiere fotografato da me l’estate scorsa. Non vi sembra bello?

 

 

Proprio mentre stavo scrivendo questo articolo, ho letto il libro molto bello di Stefano Mancuso “Fitopolis: La città vivente“, in cui l’autore ci invita a immaginare una città in cui gli alberi possono colonizzare soprattutto le strade cittadine e i centri storici. Mancuso offre una prospettiva illuminante sull’integrazione del verde nelle città e dimostra come la progettazione sostenibile e la promozione della biodiversità possano coesistere con l’urbanizzazione. La realizzazione di tali concetti potrebbe fungere da modello per la creazione di città più belle e vivibili.

Il verde nelle città non è più solo un’opzione estetica, ma una necessità imprescindibile per affrontare sfide urbane complesse. Fortunatamente, stanno emergendo molteplici vie per trasformare gli ambienti urbani in luoghi più sani, sostenibili e armoniosi. Questo rivela una tendenza crescente verso un’urbanizzazione equilibrata, in cui l’uomo e la natura si influenzano positivamente a vicenda. La sfida ora è coltivare e diffondere queste pratiche, affinché il verde possa continuare a prosperare nelle città del futuro.

Ricevo e pubblico molto volentieri questa bellissima storia. Ogni donazione sarà gradita e ricompensata. Buon Anno!

 

Il racconto di Ostaria

L’incredibile storia di un’antica varietà di fico rinvenuta nelle terre di Bari

 

Questo racconto di fatti realmente accaduti, con personaggi e tempi reali ma dalla realtà che supera la fantasia, nasce nella primavera del 2017 da un incontro fortuito con un uomo eccezionale… ma spero che questa storia non finisca mai.

I nomi delle persone, per un corretto problema di privacy, sono di fantasia.

Paolo Belloni

I Giardini di Pomona (https://www.igiardinidipomona.it/)

1 gennaio 2024

 

***

L’incontro con Lorenzo, personaggio straordinario

“Vedrai, ti piacerà” – stavo parlando con un visitatore de “I Giardini di Pomona” che, come a volte accade – mi aveva suggerito di visitare un vivaio specializzato in frutta antica in un paese vicino a Bari. Oltre alla visita del vivaio mi consigliava di conoscere il proprietario.

Incuriosito, misi in programma di andarci il primo pomeriggio libero.

Giunto alle porte del paese, trovai con qualche difficoltà l’insegna del vivaio all’ingresso di una abitazione privata. Mi addentrai nel vialetto d’ingresso che costeggiava la casa e mi trovai immerso in un coacervo di piante in vaso, altre messe a dimora in terra piena, carrelli per il trasporto, una rimessa coperta, sorretta da pilastri ma aperta sui lati, piena di attrezzi, di sacchi di terriccio, di piante da consegnare ed ebbi la netta sensazione di trovarmi immerso in un luogo di lavoro – forse di… troppo lavoro da poter compiere da soli – come se i progetti da realizzare fossero superiori alle energie disponibili.

A un certo punto comparve Lorenzo, il proprietario. Subito fui colpito dal suo sguardo: un misto di dolcezza, vivacità, determinazione, curiosità, serenità ed empatia. Un uomo anziano, di statura media, che doveva esser stato di grande bellezza e che ancora emanava una sorta di raffinato fascino contadino, assolutamente privo di orpelli.

Subito mi condusse nel suo vivaio-bosco-giardino. Un luogo che trasudava raffinatezza, ordinato disordine, passione, tradizione e ricerca.

Ci addentrammo tra piante in vaso raggruppate per specie, cespugli di canne che celavano melograni ottenuti da seme, agrumi storici, flora spontanea, piante ornamentali e piante rare. Era come se il vivaio fosse l’emanazione del suo approccio funzionale al mondo vegetale: assolutamente libero da convenzioni e da qualsiasi schema o pregiudizio.

La conversazione entrò subito nello specifico: parlammo delle varietà di mele e pere antiche che conoscevamo entrambi e condivisi alcuni suoi giudizi molto acuti su pregi e difetti delle stesse.

La prima impressione che ebbi di lui, mai smentita in seguito, fu quella di trovarmi di fronte a un personaggio straordinario, con una vastissima esperienza nella coltivazione, moltiplicazione e cura delle piante, ancora divorato dal desiderio di conoscere e sperimentare, privo di qualsiasi gelosia delle proprie scoperte, ma, al contrario, colmo di un generoso desiderio di condividere questo enorme patrimonio di conoscenze accumulato nella sua lunga vita passata tra le piante con tutti coloro che fossero disposti a riceverlo e farlo proprio.

Insomma, la persona che mi sarebbe piaciuto aver avuto come maestro.

Era come se Lorenzo avesse le capacità di certi curanderos sudamericani che, per curare un paziente, assumono e gli fanno assumere funghi allucinogeni per entrare in sintonia profonda con lui, visualizzare la malattia e la pianta da usare per curarlo. Ecco, era come se Lorenzo avesse la loro stessa capacità istintiva di entrare in connessione profonda con il mondo vegetale senza bisogno di alterare con altre sostanze il proprio stato mentale. Capiva immediatamente ciò di cui una pianta aveva bisogno e cercava di assecondarla.

A questa prima visita ne seguirono altre, venne a trovarmi più volte a “I Giardini di Pomona” da solo o con amici e nacque una buona amicizia sostenuta da reciproca stima.

 

Un fico di nome Ostaria

Un giorno di ottobre andai a trovarlo per portargli il mio libro Fichi di Puglia che mi aveva chiesto e mi fece trovare un magnifico cesto di frutti autunnali. La loro dovizia, l’eleganza delle forme e dell’abbinamento dei colori, la promessa di sapori antichi e la cura nella composizione non mi fecero notare, al momento, uno spazio minuscolo in cui erano incastonati alcuni piccoli fichi bruni essiccati che, tornato a casa, trovai assolutamente squisiti.

Incuriosito gli telefonai per chiedergli il nome della varietà e come avrei potuto procurarmi le sue talee. Mi disse che il fico si chiamava Ostaria ed era una varietà locale con fichi molto piccoli nata da un seme fortunato probabilmente cresciuto vicino a una vecchia osteria. Da qui, come spesso accade, il nome. In ogni caso, si trattava di una varietà antichissima praticamente estinta di cui un suo amico aveva ancora un enorme albero.

Poiché ritengo che la funzione del fico non sia più quella di sfamare la gente – come è stato in passato, basti pensare al suo ruolo di colonna portante nella dieta mediterranea – ma si sia trasformata in quella di sfizio gourmand che provoca meraviglia per la vastissima gamma di sapori che esprime, da anni sto cercando fichi di piccola pezzatura ma con grande carattere.

Gli chiesi quindi di procurarmi qualche talea di questa varietà che vedevo funzionale alla mia ricerca.

 

L’avventura della riproduzione

Un giorno di maggio dell’anno seguente Franco mi telefonò informandomi che mi aveva moltiplicato Ostaria. Mi donò un vaso basso di grande circonferenza ripieno di piccole talee radicate, già con le prime foglioline. Ero colmo di gioia. Il giorno dopo lo impiegai a separare una per una le piccole talee, districando delicatamente le radichette e travasando le piantine in singoli vasi. Ormai avevo più di 20 piante in vaso. Non aspettavo altro che vederle andare a frutto per conoscere il sapore di quel fico fresco, visto che lo avevo gustato solo da essiccato. Nel giro di un paio d’anni, le piantine, cresciute bene, erano diventate alberelli.

In quel periodo frequentavo un amico che aveva realizzato in Basilicata un impianto di fichi da produzione. Da trent’anni mi battevo per il ritorno alla coltivazione del fico nel Sud Italia e mi parve il raggiungimento di un traguardo. Subito gli proposi di abbinare al suo impianto una produzione di nicchia con quattro varietà di fichi piccoli scelte da me, selezionate tra le oltre 500 varietà da me coltivate. Tra queste, l’ultima arrivata Ostaria.

Subito si rese disponibile ed io seguii la messa a dimora delle piante. Per precauzione mi ero tenuto qualche vaso di Ostaria che piantai in una nuova foresta alimentare in aridocoltura – la numero tre – che stavamo realizzando a Pomona.

Nel frattempo, il Covid aveva rallentato la mobilità e quando, lo scorso anno, appena possibile, tornai in Basilicata a visitare l’impianto, constatai con costernazione che non era restato nulla. Tutte le piante, abbandonate a loro stesse, erano morte. Il viaggio di ritorno fu un misto di dolore profondo, senso di smarrimento e grande rabbia.

Il ’22 era già stato un anno disgraziato. Moltissime delle varietà messe a dimora nei due anni precedenti, frutto degli ultimi 5 anni di lavoro di recupero, erano morte a causa del grande calore estivo e della prolungata siccità. Non avere i soldi per un impianto di irrigazione e le forze per irrigare a mano come avevamo fatto per tutta l’estate 2021, in cui c’erano due ragazzi del Servizio Civile Nazionale ad aiutarci, aveva comportato la scelta drammatica di abbandonare il giovane impianto con circa 200 varietà.

Questa decisione grave, presa insieme a Marcello, il mio più stretto collaboratore, era stata una scelta obbligata. Ci consolammo dicendoci che alla fine avremmo scoperto quali specie fossero più resistenti alla siccità. Una magra consolazione. In effetti scoprimmo che tra fico, melograno e giuggiolo – le tre principali specie di fruttifere piantumate nella foresta mediterranea in aridocoltura – quella di gran lunga più resistente era il melograno, seguita dal giuggiolo e, come buon’ultima, dal fico.

Ripercorrere le swales* della “foresta alimentare 3”, leggere le targhette con i nomi delle varietà decedute, ripensare a come ciascuna era giunta in mio possesso, le persone che me l’avevano data e la nazione di provenienza era una sorta di via crucis. Ad ogni stazione un rinnovato dolore!

 

Uno straordinario ritrovamento

La drammatica constatazione di aver perso tutte le piante di Ostaria mi spinse a mettere da parte l’orgoglio e a rivolgermi nuovamente a Lorenzo. Gli raccontai cosa mi era successo chiedendogli se mi potesse fornire nuovamente alcune talee di Ostaria. Mi invitò ad andare a trovarlo informandomi che pochi giorni prima la vecchia pianta del suo amico era stata tagliata e che sperava rispuntassero dei polloni ma desiderava che andassimo insieme a constatare la situazione.

Lo trovai leggermente invecchiato. Subito mi condusse sul posto, un’antica masseria austera. Mi fece vedere il luogo dove il grande albero era stato tagliato. Aveva qualche difficoltà a camminare. Ci sedemmo a parlare di fronte all’aia e mi raccontò dei suoi terribili dolori di schiena e del prodigioso rimedio di sua invenzione che utilizzava per farseli passare: si preparava una tintura madre di Ruta graveolens e nel macerato alcoolico aggiungeva spicchi d’aglio, timo e rosmarino insieme a del chinino che si procurava non so come da un paese dell’Est. Era da una decina d’anni che si curava sfregandosi quella pozione a sua detta miracolosa sulle parti dolenti. Si era anche consultato con un medico che gli aveva detto che “per uso esterno non era pericoloso”. Soltanto che adesso non aveva più nessuna pianta di Ruta. “E’ una colonizzatrice, te ne porto quanta ne vuoi, ama la terra povera, poi si dissemina facilmente da sola” – gli dissi.

A novembre del ’23 sono tornati a Pomona docenti e allievi di una scuola di orticoltura del Belgio per un progetto Erasmus+. Quindi abbiamo organizzato per loro tutte le attività quotidiane per lo stage di tre settimane e, tra queste, visto che avevamo subìto danni dalle arvicole, il trapianto nelle food forest di Ruta graveolens e di Scilla marittima. La prima emana un odore che tiene lontani i roditori, la seconda, se ingerita, è tossica. Durante l’espianto della Ruta affidai a Valery, un ragazzo molto sensibile e disponibile, l’incarico di preparare alcuni vasetti di Ruta ben radicata per Lorenzo.

Concluso a dicembre il progetto Erasmus+ telefonai subito a Lorenzo dicendogli che avevo la Ruta per lui. Al telefono mi informò che mi aveva riprodotto una pianta di Ostaria e se volevo dei rami. Non capii bene cosa intendesse dirmi ma, come spesso accade in Puglia, cadde la linea e mi risolsi di andare a trovarlo il prima possibile.

Mi chiedevo dove fosse andato a scovare un’altra pianta di Ostaria. Son sicuro che doveva aver messo in moto tutte le sue conoscenze determinato a setacciare tutto l’agro del paese e mezza provincia di Bari per trovare forse l’ultimo esemplare di questa varietà. Quando giunsi da lui pochi giorni prima di Natale ‘23 mi fece trovare un vaso con una pianta di circa un metro di altezza con tre gruppi di foglie verdissime. A Pomona non avevo più nessuna foglia in tutta la collezione di fichi e davanti ai miei occhi increduli avevo foglie di una verzura da mese di maggio. Mi disse che, trovata la pianta madre, aveva tenuta umida la talea irrorandola più volte al giorno con uno spruzzino, poi, esposta al sole, erano subito spuntate le foglie.

Mentre mi donava il vaso lo chiamarono al telefono, parlò qualche minuto e poi si rivolse a me informandomi che stavano per arrivare i rami e se li volevo. Aveva trovato un esemplare di Ostaria abbandonato, completamente coperto dai rovi, ma gigantesco. Per rinforzare la pianta ne aveva fatto potare la parte superiore.

Dopo poco ci raggiunse un furgone con cassone aperto carico di rami di potatura di Ostaria.

A fianco del vaso che mi ero già messo in macchina riempii completamente i sedili posteriori di rami per farne un buon numero di talee.

Dopo aver scelto insieme ai miei collaboratori il luogo dove mettere a dimora la pianta che Lorenzo ci aveva donato (un posto dove passiamo tutti più volte al giorno in modo da poterla tenere costantemente sott’occhio) abbiamo trapiantato in vaso tantissime talee, altre talee le abbiamo messe direttamente in terra con tutti i diversi sistemi che conosco: a proboscide, a ramo pluriennale interrato e a zampa di gallina.

Ora mi sento un po’ più tranquillo.

 

***

Ringrazio ancora Lorenzo per la dedizione con cui mi ha preparato uno tra i più bei regali della mia vita e penso a quanto questo regalo sia stato fatto anche a Ostaria. Lorenzo, come tutti i veri contadini, conosce esattamente l’inestimabile valore della biodiversità e, ancora una volta dalla parte delle piante, ha capito che l’unico sistema per salvare Ostaria fosse quello di darla a me perché a mia volta l’affidassi a tante diverse amorevoli mani.

 

Una donazione per salvare Ostaria

Da tutto questo è nata l’idea di un progetto ispirato a una catena di Sant’Antonio a fin di bene: a partire da oggi, con consegna a giugno ‘24, quando le piantine saranno radicate e in fogliazione, avrete la possibilità di prenotare Ostaria a partire da € 50,00. Un costo decisamente alto per una pianta di fico per quanto esclusiva, ma giustificato e accessibile per una donazione finalizzata alla conservazione della biodiversità. Chiunque acquista la pianta potrà a sua volta, se è capace di riprodurla, rivenderla al prezzo che riterrà più congruo, in modo da rifarsi del costo iniziale, oppure donarla diventando, sia in un caso che nell’altro, a sua volta attore di un sistema virtuoso di conservazione della biodiversità. Un gesto concreto che a voi consente di partecipare attivamente al progetto e a noi di recuperare altre varietà a rischio di estinzione, ricordando che la biodiversità non si salva con i convegni, ma quando le piante affondano le proprie radici nella terra madre e nutrice.

Per prenotare una piantina sarà sufficiente effettuare un versamento con PayPal: http://www.paypal.me/igiardinidipomona/50 oppure mediante

un bonifico intestato a:

Azienda agricola dimostrativa “I giardini di Pomona “di P. Belloni

IBAN: IT78X0306978934100000679003 inviando la ricevuta a: [email protected] . In entrambi i casi vanno inviati i dati per poter effettuare la consegna: nome, cognome, numero di telefono e indirizzo del luogo dove si vuole che la pianta venga consegnata. I costi di spedizione per l’Italia sono inclusi.

Se si desidera che insieme alla pianta giunga al destinatario anche questo racconto ricordarsi di inserire la mail del destinatario.

Naturalmente l’importo della donazione non ha limiti per eccesso!

Sarà nostra cura comunicarvi la data della spedizione delle piantine non appena saranno pronte.

 

Informazioni utili per i sostenitori

A partire da giugno riceverete Ostaria in un vaso 12×12. Potrete tenere la piantina nello stesso vaso fino a novembre oppure travasarla in un vaso un po’ più grande da 3 litri a fine luglio. Se volete piantarla in terra piena vi conviene aspettare la caduta delle foglie a novembre.

Le piante continuano a sviluppare le radici e durante l’inverno si adattano meglio al terreno. Così non sarà necessario prendersene cura fino alla primavera ‘25. Se si decidesse di tenere la pianta in vaso, è opportuno cambiarle vaso ogni anno, per i primi anni, aumentando progressivamente il diametro e aggiungendo il terriccio mancante. Innaffiare sempre fino a fare fuoruscire l’acqua dai fori alla base subito dopo i trapianti.

 

Consigli per la piantumazione in terra piena

Il fico è una pianta mediterranea. Scegliete di posizionarlo in pieno sole, in un luogo senza ristagni d’acqua e ad una ragionevole distanza dalla casa e da eventuali cisterne in quanto le sue potenti radici possono, allungandosi, combinare guai. Non preoccupatevi del suolo, il fico è una pianta facile che si adatta a qualsiasi tipologia di terreno (adora le rovine di cemento), è un albero parsimonioso e generoso. Consente tutti gli errori di potatura senza soffrirne troppo. L’essenziale è bagnarla per i primi tre anni da aprile a ottobre in modo che possa estendere bene le proprie radici e diventare perfettamente autonoma. Ma non abbiate timore: anche in questo caso vi segnalerà quando vuole acqua abbassando le foglie.

Quando si innaffia una pianta bisogna sempre innaffiarla con abbondanza e poi lasciarla asciugare fino a quando non vi chiederà nuovamente l’acqua. Le piante muoiono più spesso per marciume radicale che per siccità e se sono troppo viziate perdono caratteri di rusticità. Tuttavia una buona concimazione, meglio se con stallatico maturo, verrà senza dubbio apprezzata.

Il fico non teme troppo il freddo, resiste tranquillamente a -10° e neppure il vento e l’acqua salmastra. Se vi preoccupate solo di dargli da bere quando ha sete vi darà delle magnifiche soddisfazioni e, visto che può raggiungere cent’anni di età, tanti frutti per voi e le generazioni future. Poi, come scrive Carmine Abate è “l’albero della fortuna”.

Da ultimo, chi prenoterà una pianta riceverà due nuovi testi:

1. Perché il fico
2. Il fico, scrigno di tesori per la salute.

Di Luv, l’altra varietà di fico piacentino, nera come il lupo nelle favole dei bambini, che ho salvata da sicura estinzione… vi racconterò un’altra volta.