Fillotassi, serie di Fibonacci, sezione aurea e altre cose di questo genere (seconda parte)
La spirale aurea, come i numeri di Fibonacci, si ritrova spesso nel mondo vegetale e animale. L’esempio più celebre è la conchiglia del nautilo o il guscio delle chiocciole. In particolare, nel nautilo (Nautilus pompilius), la conchiglia aumenta di grandezza e si costruisce camere sempre più spaziose sigillando quelle vecchie perché diventate piccole. Come la spirale logaritmica, la forma della conchiglia non cambia forma e l’animale può cresce mantenendo le stesse proporzioni.
Ma non solo: i falchi si avvicinano alla loro preda secondo una spirale logaritmica, gli insetti si dirigono verso una sorgente di luce seguendo una spirale logaritmica, i bracci delle galassie e dei cicloni tropicali sono spirali logaritmiche, e la spirale logaritmica si può notare – e qui torniamo al post di oggi – nella disposizione delle strutture di alcune piante, cioè appunto nella fillotassi (esempi nelle figure qui in basso).
La figura in basso illustra un esempio di fillotassi spirale nel capolino di un girasole, infatti se si contano attentamente il numero delle spirali, si nota che quelle in senso orario, evidenziate in arancione, sono 21 e quelle in senso antiorario, in azzurro, sono 34, cioè due numeri consecutivi della successione di Fibonacci. In ogni caso il numero di spirali visibili nel capolino di un qualsiasi girasole è sempre dato da due numeri consecutivi della successione di Fibonacci.
E ancora, nel fiore di Arthemis tinctoria (in basso), contando le linee, si può individuare una coppia di numeri che corrispondono al numero di spirali in ciascuna direzione (13 e 21 nell’esempio), cioè due numeri consecutivi della sequenza di Fibonacci.
Ma perché avviene questo fenomeno? Quali sono le cause? Sembra che la parte attiva del fiore, quella in cui avviene la crescita vera e propria sua una zona circolare chiamata apice, posto al centro del fiore; sul bordo dell’apice si formano i primordi, che poi si sviluppano fino a diventare semi, stami o foglie. Ciascun primordio nasce ruotando rispetto al precedente di un certo angolo (come vedremo fra un po’, si tratta dell’angolo aureo). Nel caso dei fiori, lo sviluppo è essenzialmente bidimensionale e un primordio crescendo, sposta verso l’esterno i primordi più vecchi per farsi spazio. Come conseguenza di questo spostamento, i primordi sono disposti lungo una stretta spirale chiamata spirale generatrice e le spirali più larghe, enumerate dalla successione di Fibonacci, sono chiamate parastichi. Lo sviluppo geometrico del fiore dipende quindi da tre fattori: l’angolo di divergenza, la forma dei primordi e come un nuovo primordio sposta i precedenti.
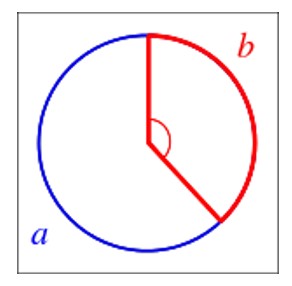
Nel 1837, Auguste e Louis Bravais osservarono che ciascun elemento botanico, sviluppandosi uno per uno, diverge di un angolo d rispetto al precedente. In molti casi, l’angolo di divergenza d approssima l’angolo aureo cioè i 137,5 gradi, che si ottiene dividendo la circonferenza stessa in due archi a e b che stanno tra loro nello stesso rapporto che si ha nella sezione aurea (figura in basso).
Questo avviene, ad esempio, per l’angolo fra due rami successivi, che segue spesso l’angolo aureo, o l’emissione di nuovi rami nel tempo, che evolve seguendo la successione di Fibonacci. Oppure ancora nell’angolo tra una foglia e l’altra in quella che si chiama appunto spirale di Fibonacci. Naturalmente non tutte le piante seguono questa regola; spesso ci sono alla base successioni che implicano il raddoppiamento dei numeri di Fibonacci oppure altre serie numeriche simili.
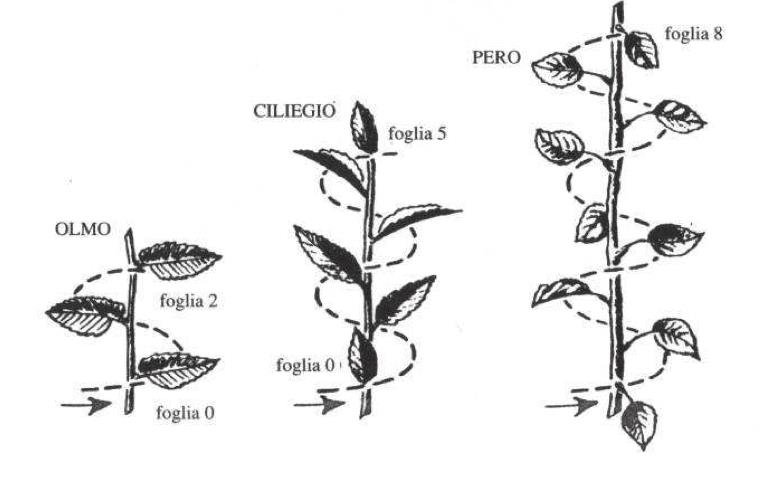Esempi di fillotassi a spirale di Fibonacci in olmo, ciliegio e pero.
In moltissime specie vegetali, la posizione in cui nasce ciascuna foglia (o fiore) all’interno del meristema, è posta ad una distanza angolare costante rispetto alla foglia che è sorta appena prima (la quale nel frattempo si sarà ingrandita e allontanata dal centro del meristema stesso). Questo angolo, formato dalla posizione di due foglie consecutive e il centro del meristema da cui sono sorte, corrisponde esattamente a 222.5 gradi (360 meno l’angolo aureo). Ciò genera una spirale che gira attorno al fusto principale. Quindi, quando le foglie saranno cresciute, girando attorno ad uno stelo e muovendosi dal basso verso l’alto, incontreremo una foglia o un fiore ogni 222.5 gradi. Infatti, se dividiamo l’angolo giro di 360 gradi per la sezione aurea otteniamo esattamente 222.5.
Nel caso delle foglie, si pensa che la disposizione a spirale di Fibonacci ottimizzi l’assorbimento della luce e della fotosintesi nel germoglio o nella chioma, promuovendo al meglio la crescita delle piante e la loro produzione. Si può ipotizzare che tale organizzazione sia correlata alla massimizzazione dello spazio oppure alla quantità media di luce incidente e di acqua piovana catturate per ogni singola foglia. L’idea rivoluzionaria di questa teoria sta nel considerare il processo di crescita della pianta come processo meccanico e non genetico. Douady e Couder, in un famoso lavoro del 1996, arrivarono all’angolo aureo supponendo che i primordi generati dall’apice meristematico apparivano a uguali intervalli di tempo seguendo una traiettoria circolare attorno al fusto. Considerarono, inoltre, che questi primordi si respingevano l’un l’altro man mano che ne nascevano dei nuovi, così da massimizzare la distanza fra essi. Secondo i due autori, le foglie emettono un segnale costante che inibisce la crescita delle altre foglie nelle vicinanze e tale segnale si indebolisce con la distanza. Questo fenomeno sembra essere legato alle auxine, ormoni che regolano crescita e sviluppo degli organismi vegetali. L’accumulo di auxina in particolari regioni del meristema sarebbe quindi il segnale che determina la posizione in cui verrà iniziato il differenziamento della nuova foglia. Allo stesso tempo, l’ormone verrà attivamente trasportato verso la nuova fogliolina producendo una forte riduzione della sua concentrazione nelle regioni circostanti. Ogni foglia è così circondata da una zona a bassa concentrazione di auxina che funge da campo inibitore, impedendo la formazione di altre foglie nelle vicinanze. Sarà quindi necessario attendere che i primordi crescano e si allontanino dal centro del meristema con il passar del tempo (definizione temporale) afinché ci sia una concentrazione di auxina sufficientemente alta da consentire l’instaurarsi di un nuovo primordio (definizione spaziale). L’effetto combinato di attivazione e inibizione del differenziamento regolato da questo ormone, determinerebbe quindi la geometria a spirale di Fibonacci. Ad esempio, i fiori e i semi il cui differenziamento avviene secondo questo stesso criterio geometrico risultano disposti in modo molto compatto, così da ridurre al minimo gli spazi vuoti tra una struttura e l’altra. In questo modo i primordi si organizzavano in un modello spaziale regolare altamente efficiente. Ad esempio, se osserviamo l’immagine in basso e teniamo conto dei campi inibitori generati dai primordi 8 e 9, noteremo che la posizione favorita per la formazione di una nuova foglia è esattamente quella in cui si sta formando il primordio 10. In alternativa, l’impaccamento efficiente dei primordi nel meristema potrebbe avere un ruolo protettivo dei primordi da sollecitazioni ambientali. Da una prospettiva strutturale, i regolari modelli di fillotassi possono bilanciare le forze che le foglie esercitano sullo stelo. In questa ottica, la regola empirica di Hofmeister può essere facilmente spiegata assumendo che ogni primordio sia la fonte di un inibitore che diminuisce in forza con il tempo e/o la distanza. Il nuovo organo si presenta quindi nel sito dove l’inibizione è più bassa all’interno della zona periferica.
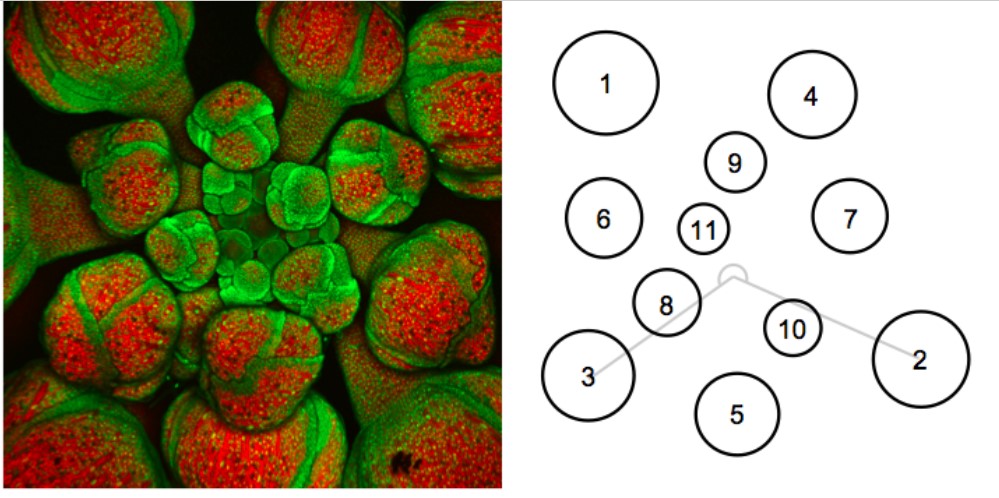Immagine al microscopio del meristema apicale di Arabidopsis sulla sinistra e rappresentazione schematica della posizione dei boccioli sulla destra. I fiori più giovani sono al centro, mentre quelli più vecchi, più grandi, sono spostati verso l’esterno. L’angolo che si forma tra un bocciolo e quello successivo corrisponde esattamente a 222,5°. Fonte: PLoS Biology Issue Image, PLoS Biol 8(5): ev08.i05.
Per concludere, la fillotassi basata sui numeri di Fibonacci potrebbe apparire come una necessità matematica che deriva dalla combinazione di un apice espanso e di un adeguato meccanismo di spaziatura per il posizionamento di nuove foglie. Tuttavia, lo stesso meccanismo si applicherebbe ugualmente bene all’esaurimento o alla concorrenza di un composto da parte delle foglie in via di sviluppo, e potrebbe senza dubbio includere altre sostanze oltre alle auxine. A causa di tutta questa complessità, i principi matematici coinvolti sono chiari quando si assume che solo due foglie a contatto influenzino una foglia nuova. Ciò nonostante, questa non è una precondizione della fillotassi di Fibonacci, dal momento che modelli informatici hanno mostrato che questo andamento si genera anche quando molte foglie contribuiscono all’inibizione su un punto preciso. Nonostante ciò, il modello di Fibonacci sembra essere un fenomeno robusto e stabile; un indizio che va nella direzione della sua presenza così diffusa tra le piante. Ci sono però modelli matematici che descrivono anche altri schemi a spirale diversi da quelli di Fibonacci, meno comuni ma comunque presenti in natura. Munetaka Sugiyama, coautore di un articolo pubblicato recentemente, ha spiegato di aver modificato il presupposto fondamentale, per cui il potere inibitore non è costante ma cambia con l’età e le foglie più vecchie possiedono un effetto inibitore più forte nei confronti dei nuovi primordi. I modelli matematici basati sull’inibizione reciproca possono ricreare gran parte dei modelli fillotassici osservati. I ricercatori stanno quindi cercando di progettare un nuovo concetto che possa illustrare tutti gli schemi conosciuti di fillotassi e non solo alcuni di essi. Il futuro ci riserverà di sicuro nuove risposte, e probabilmente anche nuove domande su questo affascinante argomento!
Grazie a loro, ho scritto:
Charles Darwin (1875) On the Movements and Habits of Climbing Plants.
Cris Kuhlemeier (2007) Phyllotaxis. Trends in Plant Science, 12(4), 143-150. doi: 10.1016/j.tplants.2007.03.004
Didier Reinhardt (2005) Regulation of phyllotaxis. Int. J. Dev. Biol. 49: 539-546.
Fernando Valladares, Daniela Brites (2004) Leaf phyllotaxis: Does it really affect light capture? Plant Ecology 174: 11–17.
G J Mitchison (1977) Phyllotaxis and the fibonacci series. Science 196 (4287): 270-275.
Jean M. Gerrath, Usher Posluszny (2007) Shoot architecture in the Vitaceae. Can. J. Bot. 85: 691–700.
La sezione aurea, la serie di Fibonacci e la natura. Marzo 2013. Settimana della cultura scientifica e tecnologica – 8° edizione. IIS “Ettore Majorana” di Avezzano. Scarica qui.
Laura Resta (2010) La successione di Fibonacci nella fillotassi. Tesi di Dottorato. Alma Mater Studiorum Bologna.
Richard S Smith, Soazig Guyomarc’h, Therese Mandel, Didier Reinhardt, Cris Kuhlemeier, Przemyslaw Prusinkiewicz (2006) A plausible model of phyllotaxis. Proc Natl Acad Sci U S A 103(5): 1301-1306.
Ron Knott, Fibonacci numbers in nature (2009) https://rknott.surrey.ac.uk/Fibonacci/fibnat.html
Siobhan A. Braybrook, Cris Kuhlemeier (2010) How a plant build leaves. The Plant Cell, Vol. 22: 1006–1018
Soren Strauss, Janne Lempe, Przemyslaw Prusinkiewicz, Miltos Tsiantis, Richard S. Smith (2020) Phyllotaxis: is the golden angle optimal for light capture? New Phytologist 225: 499–510.
Sarlikioti, P.H.B. de Visser, G.H. Buck-Sorlin, L.F.M. Marcelis (2011) How plant architecture affects light absorption and photosynthesis in tomato: towards an ideotype for plant architecture using a functional–structural plant model. Annals of Botany 108: 1065–1073.
Yannick M. Staedler, Peter H. Weston, Peter K. Endress (2007) Floral Phyllotaxis and Floral Architecture in Calycanthaceae (Laurales). International Journal of Plant Sciences 168(3): 285-306.
